摘要:本文詳細闡述了從CIE RGB色坐標圖到CIE XYZ色坐標圖的轉換過程。由于RGB色坐標存在負值問題,因此引入了新的顏色標準XYZ。文章首先介紹了制定新顏色標準時的三個條件,然后詳細推導了從RGB到XYZ的轉換公式。通過假設和聯立方程,求得了XYZ在RGB色度圖中的坐標,并得出了XYZ和RGB三刺激值之間的關系。最后,通過將RGB色坐標圖中的色坐標帶入得到的公式中,完成了兩種色坐標圖之間的轉換。
自己做的一個總結,然后有其他的小伙伴以后遇到相同的問題的話希望有用,當然其實應該是沒有人看的。
那就,開始了?
首先看一下CIE RGB色坐標圖和CIE XYZ色坐標圖,由于RGB中存在負值問題,所以就有了新的顏色標準XYZ,以此解決負值問題。
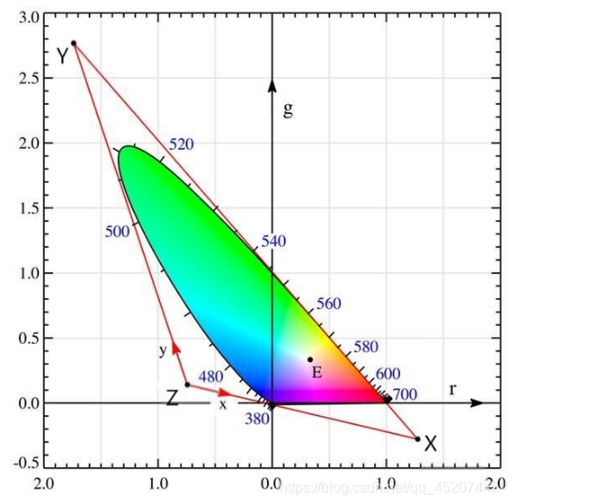
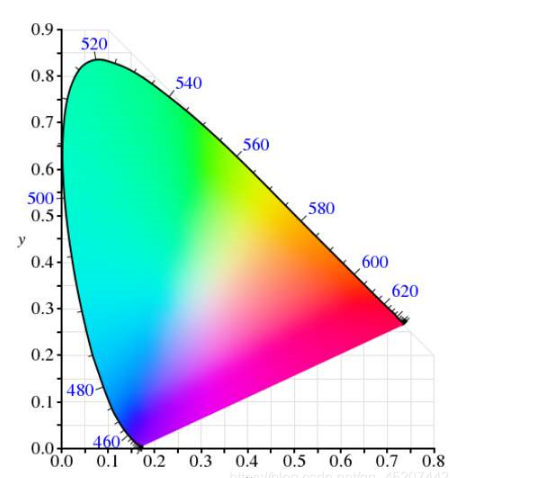
首先說一下,在制定新的顏色標準時提出了三個條件,分別是:
1.三刺激值均為正
2.某一原色的刺激值正好代表混合色的亮度,而另外兩種原色對混合色的亮度沒有貢獻(后來就選中了Y,所以Y其實代表了混合色光的亮度)
3.當三刺激值相等時,混合光仍代表標準(等能)白光
接下來就要開始推導怎么從第一幅圖到第二幅圖了!
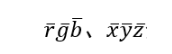
先假設:RGB、XYZ分別為兩種顏色空間的三原色的單位,分別為三刺激值,rgb、xyz為歸一化后的值,即:(公式好難打,我就直接貼word里的圖了)(評論里的小伙伴說了另一種表示的方法,其實只是用不同的符號表示而已,那位小伙伴的表示法會用的更多一點,而我是因為當時老師的作業用的是這種表示法)
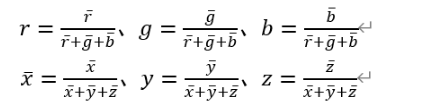
由于XYZ可分別由RGB混合得到,所以:
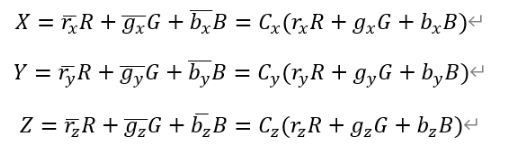
其中:
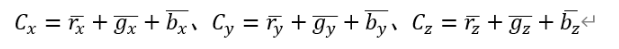
在RGB得到的偏馬蹄形圖中,為了滿足提出的三個條件,我們可以分析得到
取Y的刺激值表示混合光的亮度,則X、Z都只表示色相而無亮度,即X、Z處于無亮度線上,即:
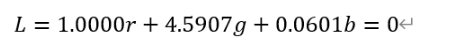
又因為:
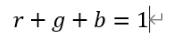
聯立兩個式子就可以得到第一張RGB圖像中的直線XZ的方程:
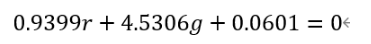
2.由于要使三刺激值都為正,所以新組成的三角形XYZ要包含圖中所有的彩色點,所以可以分別取XY、YZ直線為:
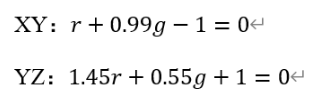
聯立三條直線的方程就可以解得XYZ在RGB色度圖中的坐標:
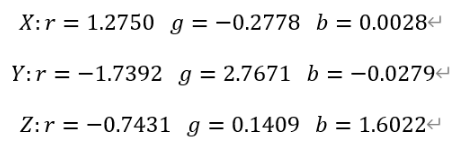
由于上面的得到的是在色度圖中的坐標,是經過了歸一化的,所以真實的XYZ用RGB表示的三刺激值應該乘上C,即:

對上面的矩陣求一個逆矩陣就可以將RGB用XYZ表示,即:

其中A是相應的C的倒數。
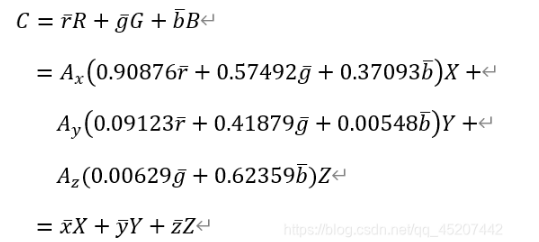
由于任意一種顏色C都可以用RGB和XYZ顏色空間進行表示,所以可以得到以下的關系:
所以XYZ和RGB的三刺激值之間的關系為:
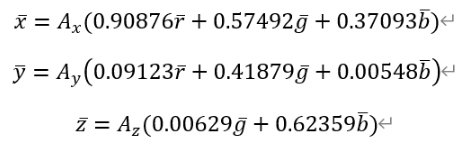
接下來我們要做的就是求出A了!
由前面得要求二可知Y的刺激值表示的是混合色的亮度,且已知當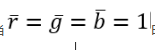 時的混合色為等能白光,亮度L=5.6505,帶入
時的混合色為等能白光,亮度L=5.6505,帶入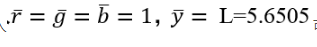 可解得:
可解得: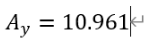
又由于要求三知等能白光時XYZ空間也有三刺激值相等,所以此時還有: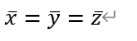
帶入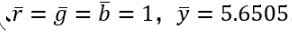 可解得:
可解得: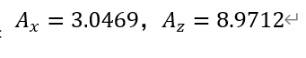
所以兩種顏色空間三刺激值之間得關系為:
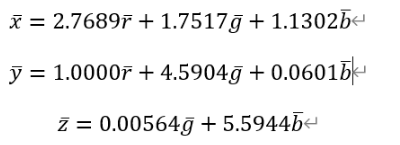
因為色坐標圖是經過歸一化得,所以歸一化后的關系為:
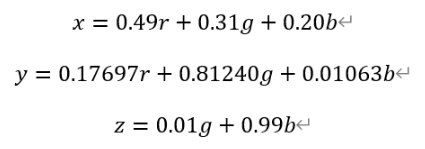
到這一步,我們就可以把之前RGB色坐標圖中的色坐標(r,g)帶入上面的式子中得到XYZ色坐標圖中的色坐標(x,y),就完成了最前面兩幅圖之間的轉換了!