sRGB色彩空間是一種標準的RGB色彩空間,廣泛應用于顯示器、打印機以及因特網等領域。它將紅、綠、藍三原色的顏色定義為在CIE xy顏色坐標系中的特定位置,并通過非線性變換將原色強度與實際保存的數值之間進行轉換。這種設計使得sRGB能夠高效地表示人眼可以分辨的顏色。
要將sRGB色彩空間中的RGB值轉換為LAB值,需要進行一系列的計算。LAB色彩空間是一種基于人眼對顏色的感知而設計的色彩空間,其中L表示亮度,A和B表示色彩的兩個維度。下面是一種常用的方法來進行RGB到LAB的轉換:
? ? 1.將sRGB中的RGB值轉換為線性RGB值。sRGB使用非線性變換來保存圖像文件中的數值,因此需要將其逆變換為線性RGB值。這可以通過應用sRGB的逆gamma校正公式來實現。
? ? 2.將線性RGB值轉換為XYZ值。XYZ色彩空間是一種與設備無關的色彩空間,可以作為RGB和LAB之間的橋梁。通過將線性RGB值乘以適當的轉換矩陣,可以得到對應的XYZ值。
? ? 3.將XYZ值轉換為LAB值。最后一步是將XYZ值轉換為LAB值。這涉及到一些復雜的數學計算,包括對數函數和冪函數的運算。具體的轉換公式可以在相關的色彩科學文獻中找到。
需要注意的是,這些轉換過程涉及到浮點數運算,因此在實際應用中可能需要進行適當的數值處理和近似計算。此外,色彩空間的轉換也可能受到顏色管理系統的影響,因此在實際應用中可能需要根據特定的需求和標準進行調整和優化。
條條大路通羅馬,就像我們可以用5+5來表示10,也可以用2x5來表示10,甚至是20-10也可,同樣一種顏色,也可以用不同形式來表示。不同的形式有不同的優缺點,對于色彩空間來說,不同的空間能表示的色域是不同的。
用一個例子可以很好的理解不同的色彩空間以及他們之間的區別:假設有兩個色彩空間,它們分別是R1 G1 B1和R2 G2 B2。現在我們的目標是,找到兩個色彩空間之間的映射關系。現在我們已知R2 G2 B2 [1 0 0]的顏色情況,還有一個R1 G1 B1的顯色器,若我把R1 G1 B1也設置成[1 0 0],會出現這么個情況:(上標表示的是R1 G1 B1,下標表示的是R2 G2 B2)
顯然,這兩個不同的色彩空間,那么通過調整R1 G1 B1,也可以使兩種顏色一樣,只不過確實要慢慢試:

那么根據此,我們可以得到以下的關系式:
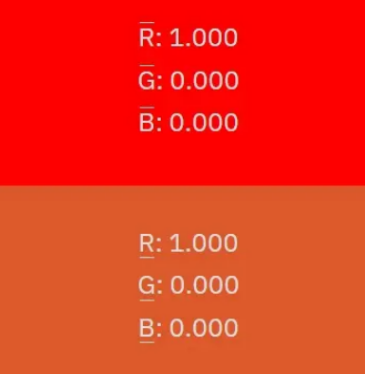
R1 = R2 * 0.712
G1 = R2 * 0.100
B1 = R2 * 0.024
對R2 G2 B2 [0 1 0]和R2 G2 B2 [0 0 1]也是同理:
得到的關系式就分別是:
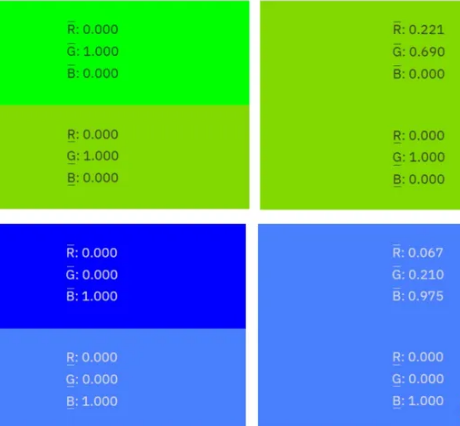
R1 = G2 * 0.221 ; R1 = B2 * 0.067
G1 = G2 * 0.690 ; G1 = B2 * 0.210
B1 = G2 * 0.000 ; B1 = B2 * 0.975
目前我們只知道R2 G2 B2為純色的時候,R1 G1 B1分別要顯示的量,那么如何確定非純色的時候,R1 G1 B1要如何分配呢?比如說R2 G2 B2[0.9, 0.5, 0.2]的時候?
這個時候就要祭出我們的色覺尚方寶劍,格拉斯曼定律(Grassmann's laws),其內容是:人類對色彩的感知是線性的,即如果兩個顏色的光匹配,此時添加另一組匹配的光,他們的總和也是匹配的。這里的匹配是指在一個色彩空間當中。
也就是說,我們已經知道R1 G1 B1分別與R2、G2、B2的關系,那么要求R1 G1 B1與R2 G2 B2的關系,我們只需要將其線性相加即可:
R1 = 0.712 * R2 + 0.221 * G2 + 0.067 * B2
G1 = 0.100 * R2 + 0.690 * G2 + 0.210 * B2
B1 = 0.024 * R2 + 0.000 * G2 + 0.976 * B2
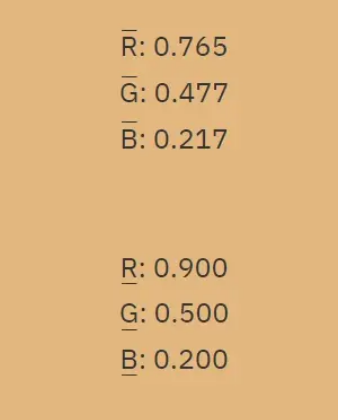
那么我們解決上面的問題,當R2 G2 B2[0.9, 0.5, 0.2]時,把數值帶入上式,得到其對應的R1 G1 B1為[0.765, 0.477, 0.217],來驗證一下:
Amazing!我們再來進一步深入,那么假如我知道R1 G1 B1的值,要求R2 G2 B2對應值咋辦呢,解一個三元一次方程也不是不行,我幼兒園的表弟也是這么想的。其實這里如果引入線性代數的知識,一切都會簡單很多。
R1 G1 B1與R2 G2 B2的關系可以表示成:

那么根據小學二年級的線性代數知識,兩邊同時左乘A矩陣的逆,就可以得到:
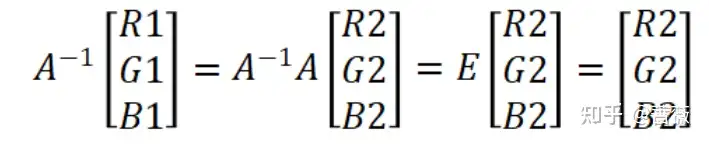
那么求出A矩陣的逆之后,不難得到:
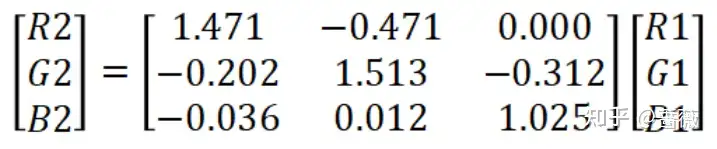
什么?你不會求矩陣的逆?哪里難了,有的時候找找自己的原因,這么多年了知識漲沒漲,有沒有認真學習(狗頭
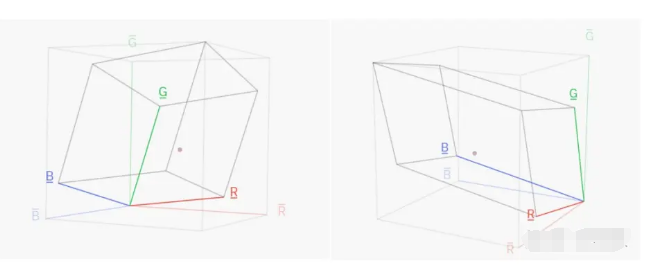
不廢話,至此,運用了線性代數的知識后,我們不難發現,所謂不同的顏色空間之間的轉換,無非就是向量基之間的轉換罷了,我想這個概念應該學過線代的都很熟悉。那么如果把R1 G1 B1作為標準坐標系,繪制出的R2 G2 B2如圖。并根據上面推出的關系繪制出的立體空間,空間內的任意一點都能表示一種顏色。那么顯然,R1 G1 B1的立體空間更大,證明R1 G1 B1色彩空間中包含的顏色也會更多。
如果把R2 G2 B2作為標準坐標系,繪制出R1 G1 B1坐標系,得到的結論也是一樣的:
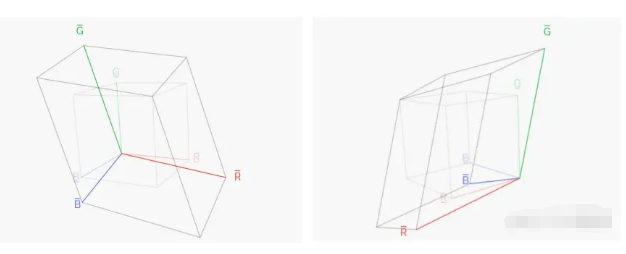
(如果覺得圖很抽象看不懂,可以去這個網站里自己體驗一下)
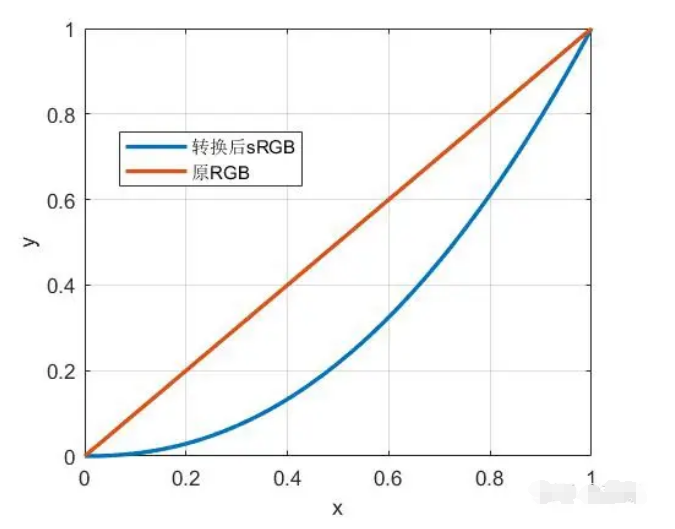
sRGB全稱standard Red Green Blue,是一些影像巨頭共同開發的一種彩色語言協議,其換算的公式本質就是一個γ值為2.2的gamma變換。至于為什么是2.2,這個和CRT(陰極射線管)顯示器的工作原理相關了,不同的顯示器gamma值也會不同,這里先按下不表。
gamma變換的公式為??,如圖:
若一個像素的RGB值(歸一化后)為[0.1, 0.2, 0.3],那么輸出的sRGB就是[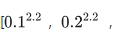
 簡單易懂嗷兄弟們。
簡單易懂嗷兄弟們。
當然對此也有更深的理解,小學學過CV或者數字圖像處理的同學應該知道,gamma變換通常與圖像的對比度掛鉤。當γ值大于1的時候,圖像是整體變暗的。看起來和RGB沒啥區別,那為什么好好的RGB不用,偏要整個sRGB出來呢?
這是因為我們人眼的視覺規律是非線性的,即人眼對暗域的變化更加敏感,下面來一個生動形象的例子:已知下面兩張圖最左邊的色塊和最右邊的色塊RGB分別為[0 0 0]和[255 255 255],請問中間一部分的色塊哪塊最接近[128 128 128]?


我問了我身邊的一些非相關專業的同學,基本都是選擇了圖一的左3和圖二的第5個。如果結果和這個差不多朋友,恭喜你,你的眼睛是正常的。但是實際情況是什么?


如果非說要有個正確答案,那是圖一的第5個和圖二的右3。通過這個例子應該不難理解,人眼會覺得圖一右側的四張圖亮度的差距會比左側四張圖的差距小,換句話說就是人眼對暗處的亮度變化更加敏感。而圖二正是圖一的RGB轉成sRGB后的情況,所以人眼會覺得中間才是最接近[128 128 128]的,很好的證明了sRGB是符合人眼特性的。
XYZ是另一種表示顏色的方法,也叫三刺激值。在了解XYZ的由來以及含義前,非常有必要先知道,人眼是如何感知顏色的。目前大多人認可的是“階段學說”,在人類的視網膜上有三種不同的感光錐體,因此可以使用三種顏色(但不是我們說的三原色RGB,至于為什么不是我下面解釋)進行混加使得大腦呈現所有的顏色。當然混加也不是單純的線性,而是一個復雜過程,這里有機會再深入學習一下(給自己挖個坑立個flag)。
重要的是,人類視覺系統的三色性,到底是哪三色?CIE為了探究這個答案,做了人眼色覺匹配實驗,得到了如下圖的結果。x軸是不同波長,y軸是歸一化后的強度。
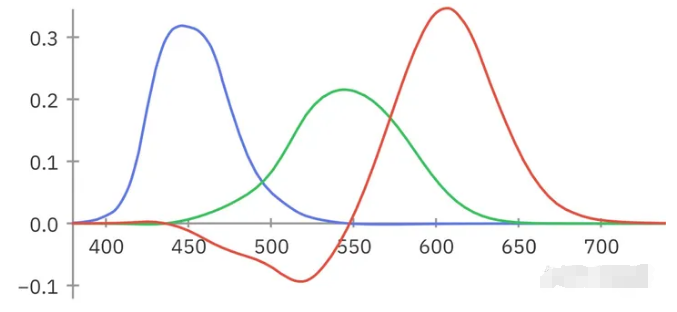
第一眼看這圖,咋還有負數,這部瞎扯淡嘛,虛空的紅?其實這就是為什么人類視覺系統的三色性中的三色(下面就簡稱三色)不是RGB的原因。
首先這張圖的x坐標代表的是波長,在小學二年級的光學里我們就知道,對應于單一波長的顏色稱為光譜顏色,也就是說,這個是我們定義顏色(無論在你腦子呈現的是什么顏色),例如波長為570nm的電磁波它就是純黃色。這里有一點要注意,顏色之間沒有一個硬性的界限,說過了這個波長它就是什么顏色,也就不存在單一的“光譜紅色”。所以說了那么多p話,總結一句就是,如果把RGB作為三色,就會出現這樣的負數問題證明普通RGB真不行。
我來舉個例子:回顧一下我一開始舉的兩個色彩空間的例子,R1 G1 B1和R2 G2 B2,我們知道,R1 G1 B1色彩空間包含的顏色是比R2 G2 B2大的,那么如果R1 G1 B1為[1 0 0],我怎么用R2 G2 B2來表示呢?你會發現,就算R2拉滿,仍然不夠紅,如果把數據直接帶到公式里面計算,則R2 G2 B2就為[1.471, -0.471, 0]。R2超出了1很好理解,就是R2 G2 B2顏色空間中的紅不夠嘛。這個負數就很抽象了,他與上面實驗出現的負數有著異曲同工之妙。

上圖是R2 G2 B2[1 0 0]和R1 G1 B1[1 0 0],顯然,左邊是不夠紅的,但其實也可以理解成,右邊是不夠綠的,那么我們可以再右邊加上一點綠,直至兩邊的顏色看起來相同,用式子能更直觀:

1.0 * R1 + 0.0 * G1 + 0.0 * B1 = (TARGET) + 0.2 * G1
(我們隨便假設是0.2吧,反正就是適量)
然后我們再將式子進行移項,也就可以得到:
1.0 * R1 + 0.0 * G1 + 0.0 * B1 - 0.2 * G1 = (TARGET)
通過閱讀式子,我們可以知道,要想將左側的顏色與右側的目標顏色匹配,則需要在左邊加上負量的綠光。從線性代數的知識也能理解,我們回顧以下這張圖:
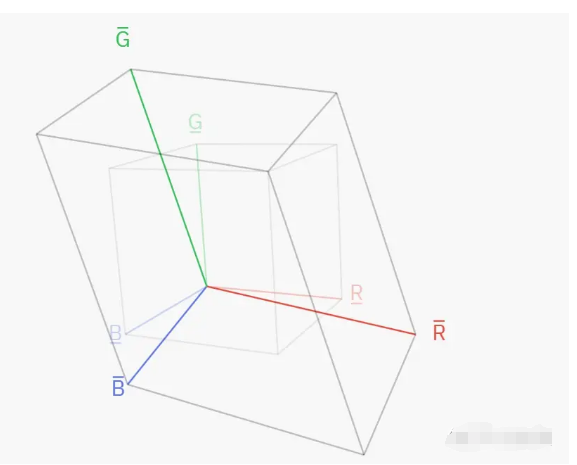
如果顏色點在R1 G1 B1和R2 G2 B2點內,那么不會出現負量的情況。但如果顏色點在R1 G1 B1內,在R2 G2 B2外,顯然,R2 G2 B2一定會出現負數才能表示該顏色點。
當然,負量在現實世界上是無法做到的,就像XYZ一樣(雖然XYZ色彩空間也不存在負量),不存在一個特定的顏色能表示XYZ或者說負量是沒有實際物理意義的,但是很多的顏色空間都是數學模型,從數學上來說是完全可行的,只要我們最后再將這個色彩空間轉換回物理顯示器能顯示的色彩空間(比如說sRGB)就可以了。實際上圖像的傳輸也確實是這個流程。
我們回到正題,CIE將實驗的R光波長定為為700.0 nm,G光為546.1 nm,B光為435.8 nm。我以570 nm作為例子,從顏色匹配圖中可以看出,匹配570nm對應的顏色需要 0.16768 個單位的 R、0.17087 個單位的 G 和 -0.00135 個單位的 B。一組三個 RGB 坐標可以表示成一個三位的坐標,那么把所有的顏色都繪制在一個三維的坐標系上,可以得到下圖的結果:
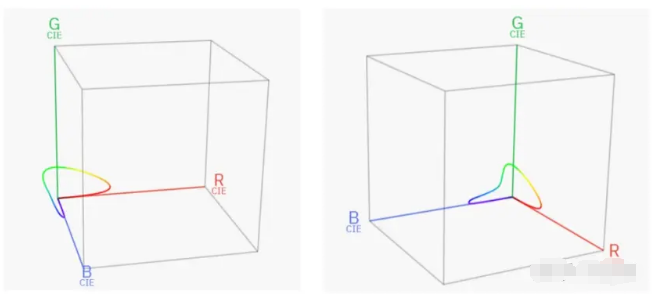
一條優美的曲線!只不過有負量存在,那么為了將這個“人眼色覺”空間轉化成一個合理的色彩空間(這里的合理一是指沒有負量,二是指將色度和亮度分離),CIE創建了以下方程組:
X = 2.769×R + 1.752×G + 1.130×B
Y = 1.000×R + 4.591×G + 0.061×B
Z = 0.000×R + 0.057×G + 5.594×B
其中Y分量是亮度分量,而 X 和 Z 定義色度。
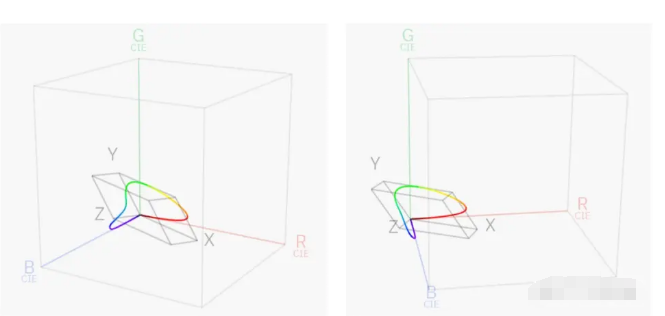
把XYZ作為直角坐標系,能更直觀的看出這個色彩空間是合理的(主要是沒有負量)。
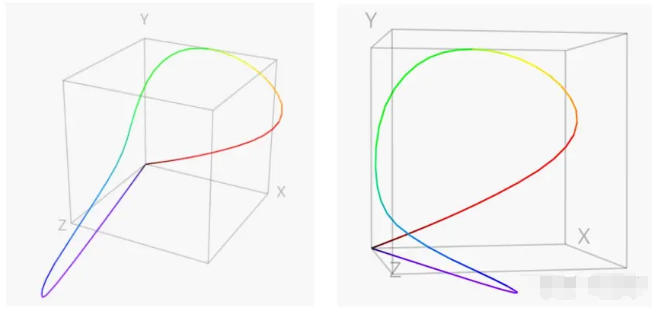
至此,咱們就有一個基準顏色空間了,即任意兩個色彩空間,我們現在不需要知道他們之間是如何轉換的,只需要能夠將它們都轉換到 XYZ 空間就行了。